質量保存式と運動量保存式は、それぞれ、物質の質量と運動量が容器内で常に一定であることを保証する式である(図1)。運動量保存式は、言い換えれば、容器内の微小領域にかかる力が常に釣り合っている状態を保証する式である。エネルギー保存式は、容器内のエネルギーの保存を保証する式であるが、マントル対流のシミュレーションでは、熱力学の関係式を用いて、決まった時間間隔ごとの熱輸送量の変化を記述する式(熱輸送方程式)に書き換えられる(図1)。マントル物質に含まれる放射性元素の壊変による内部発熱、粘性散逸による発熱、断熱圧縮による発熱の効果もこの方程式に含まれる。構成方程式は、容器内の微小領域にかかる応力と歪速度の関係式で、運動量保存式の粘性項に含まれる。さらに、地殻物質や始原物質などマントルと化学組成の異なる物質の移流を解くためには、これらの基礎方程式とは別に物質ごとの輸送方程式が必要となる。さらに、始原的なマントル物質が融解と化学分化によって地殻物質が形成されるといった物質の進化を解くためには、そのプロセスを再現する物理化学法則を考慮する必要がある。

図1 マントルの熱対流運動を支配する基礎方程式。(Ⅰ)流体の圧縮性が考慮されている保存式。(Ⅱ)非圧縮流体の保存式。さらに(Ⅲ)運動量の拡散(つまり動粘性率)と熱の拡散(つまり熱拡散率)が空間的に一定と仮定した式。
マントル物質の粘性率は極めて高いために、流れの慣性力が無視される。そのため、マントル対流のシミュレーションでは、熱拡散と粘性拡散の比であるプラントル数を無限大と近似し、慣性項を無視した運動量保存式と質量保存式を結合した式をSIMPLE(R)法[文献2]と呼ばれる速度場と圧力場を反復計算で補正しながら陰的に求めるアルゴリズムで解くことが多い[文献3]。二次元モデルでは渦度・流れ関数法を用いて速度場を解くこともある。熱輸送方程式の移流項の空間差分は、数値振動を防ぐために風上差分法やラックス・ヴェンドロフ法(ライス法)など、流れの状態に応じて計算精度を自動的に切り替える方法で解を安定化させる。
三次元球殻モデルの場合、地表面とコア・マントル境界(CMB)の力学的な境界条件は、通常、不透過(境界上の半径方向の速度がゼロ)と自由滑り(境界をまたぐ剪断応力の勾配がゼロ)の条件を与える。熱的な境界条件に関しては、地表面は大気や海水に冷やされてほぼ一定温度に保たれているので、任意の固定した温度(例えば0℃)を与える。一方、コア・マントル境界に関しては二種類の条件が考えられる。一つは、マントルは外核から一定の温度で加熱されているという仮定の下で、任意の固体温度(例えば2500℃)を与える条件である。もう一つは、外核からの熱流量が一定である仮定の下で、固定した熱流量を与えるという条件で、断熱の条件を与えることが多い。さらに、二次元や三次元の矩形もしくは部分球殻モデルでは、側面の力学的・熱的境界条件が必要となり、反射境界や周期境界を与える。
上述のように運動量保存式の慣性項が無視されるため、マントル対流では、温度場の初期条件を与えれば、その“瞬間”の定常速度場が求まる。通常のマントルダイナミクスの問題では、任意の温度場の初期条件のもと、マントル対流が熱的、力学的に平衡に達するまでシミュレーションを続ける。
基礎方程式を無次元化すると、さまざまな無次元パラメーターが現れる。マントル対流シミュレーションの最も重要な無次元パラメーターは、マントル対流の活発さの指標となるレイリー数である。レイリー数は温度差による熱浮力を分子に、粘性抵抗力を分母に持つ。したがって、レイリー数が大きいほど、粘性抵抗力に対して熱浮力が大きくなるので、活発な対流が起こり、流れの速度が増加する。また、地表面とCMBの熱境界層の厚さが薄くなるので、そこから発生する下降プルームと上昇プルームの太さも細くなる。また、マントルに含まれるウラン、トリウム、カリウムなどの放射性元素の壊変による内部発熱量が大きいほど対流が活発になる。
三次元球殻モデルを用いたマントル対流の数値シミュレーションは世界では1980年代半ばから行われてきた(表1)。基礎方程式の離散化法は、有限要素法、スペクトル法、有限体積法、有限差分法が用いられる。このうちスペクトル法は、流体内部で局所的に大きく変化する物理量を取り扱う場合、そのスペクトル展開に莫大な計算時間とメモリを要する。例えば、地球型惑星のマントルを構成する岩石の粘性率は温度や歪速度、化学組成の変化などによって水平方向に短い空間スケールで何桁も変化するため、マントル対流のシミュレーションではスペクトル法は有用ではない。一方、有限差分法と有限体積法は、粘性率またはその空間微分を各格子点で局所的に扱うことが可能である。
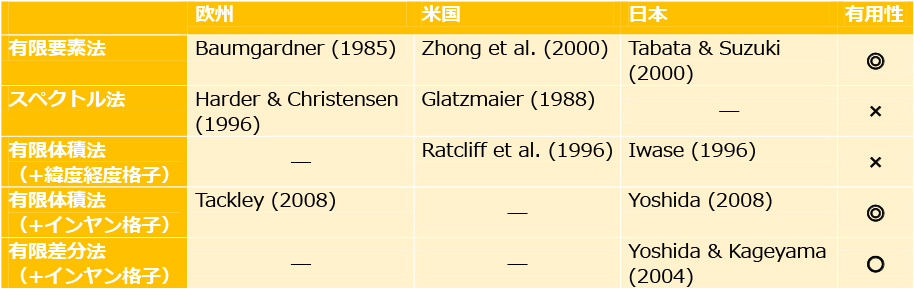
表1 これまで世界で開発されたマントル対流シミュレーションプログラムの離散化手法と、初出の論文(著者、西暦)を欧州、米国、日本別に分けている。
一般的に、規則格子(図2a)に基づく有限体積法や有限差分法は,不規則格子(図2b、c)に基づく有限要素法と比較して大規模ベクトル・並列計算機において計算効率が高いことが分かっており、マントル対流のシミュレーションでも当てはまる。有限差分法は有限体積法とは異なり、高次の差分スキームに改良することが容易であるという利点がある。一方で、有限体積法は運動量方程式に表れる粘性率の一階微分が離散化式に陽的に現れないので、有限差分法よりも粘性率の変化に強いという利点がある。また、規則格子は、地形やプレート運動データ、地震波トモグラフィーデータなど、通常、緯度経度座標データとして提供されている各種の地球物理学的観測データを容易にモデルに組み込むことができる。一方、不規則格子の最大の利点は、緯度経度座標に関係なく自由に格子を区切ることができるため、例えば地球表層の複雑なプレート境界の分布や沈み込みプレートの形状を自然な形でモデルに組み込むことができる。
規則格子を用いる場合、単純に緯度経度座標(球座標)に沿った緯度経度格子(図2a)は、二つの数値計算上の問題点が生じる。一つは両極の座標特異点の問題、もう一つは、高緯度になるほど経度方向の格子間隔が著しく狭くなる問題である。CFL(クーラン)条件による時間刻み幅は格子間隔で決定されるため、後者は特に深刻な問題である。このような“極の問題”は、緯度経度格子の低緯度領域を二つ組み合わせることで解決できる(図2d)。このインヤン格子と呼ばれるは、極の座標特異点がなく、しかも格子間隔幅が全球面にわたってほぼ均一になる[文献1]。

図2 マントル対流シミュレーションに用いられる計算格子の例。(a)緯度経度格子、(b)四面体有限要素格子[文献4]、(c)六面体有限要素格子[文献5]、(d)インヤン格子[文献3]。
スカラー量である温度、圧力、粘性率、ベクトル量である速度場の基本変数を計算格子に配置するときは、一般に、スカラー量とベクトル量を格子の中心に設置するコロケート格子法(集中格子法)と、スカラー量を格子中心に、ベクトル量を格子壁に設置するスタッガード格子法(食い違い格子法)がある。このうち、スタッガード格子(図3)は、速度ベクトルを格子壁に設置するので、各格子に出入する物質の量を、格子を再配置することなくそのまま決定することができ、また、流れの境界条件が自然に表現できるという利点があるので、マントル対流シミュレーションに採用されることが多い。

図3 スタッガード格子における速度三成分(v_r、v_θ、v_φ)、圧力(p)、温度(T)、粘性率(η)の各物理量の配置。温度、圧力、粘性率は格子の中心に、速度三成分は格子壁の中心に配置されている。有限体積法では、さらに、各格子壁の中心と各格子枠の中心に粘性率(η_1~η_6)を配置する必要がある。