マントルを構成する岩石の粘性率は、温度や圧力、歪速度、鉱物の結晶構造や結晶粒径、化学組成などに依存する。これらの要素のうち、粘性率に最も強く依存するのは温度であり、おおまかに言えば、温度が100℃下がると粘性率は1桁高くなる。したがって、温度変化が大きい地球のマントルの内部は粘性率が桁で変化する。
1990年代後半になると、コンピューターの性能と数値計算技術の向上に伴い、マントル物質の粘性率の温度依存性を考慮したマントル対流のシミュレーション研究が加速し、地球のプレート運動に似た表層運動を再現できる地球物理学的条件がかなり絞られた[文献1、2]。粘性率の温度依存性を考慮すると、マントル対流の熱・力学境界層が低温であるために粘性率が高くなり,自発的に地球のリソスフェアに似たリッド(蓋)ができる。リッドが形成される条件は地表面とマントル内部との粘性率比が3桁から4桁以上と設定した場合である[文献3]。
図1は三次元矩形内のマントル対流のシミュレーションの結果である[文献2]。このモデルでは、粘性率の温度依存性の効果と、その効果によってできたリッドが"破壊"される効果を考慮している。粘性率が高い部分は、通常、その部分に大きな応力が掛かっているので、ある値の応力(降伏応力)を超えたときに、その部分の粘性率が低くなるようにすれば、リッドに力学的に軟らかい"破壊領域"を作ることができる。降伏応力の値が十分に小さい場合は、リッドは激しく破壊され、あたかもガラスが割れたようにたくさんの小さな"破片"ができる(図1a)。一方、降伏応力が十分に大きい場合には、リッドは破壊されず、マントルの表層全体がリッドで覆われる(図1c)。この場合は、プレートテクトニクスが存在しない金星や火星の様子と同じであるといえる。
そこで、実際の地球のプレートのように、マントルの厚さよりも大きな固い蓋の"破片"を作るには、中程度の適正な値の降伏応力を与えれば良い。この降伏応力値は、リッドの破壊強度に相当する。この場合、リッドは適度に破壊され、あたかも実際の地球のプレート境界に似た線上に延びた破壊領域が生まれる(図1c)。このシミュレーション結果の場合では、モデル領域の中央付近でプレートの発散境界(海嶺に相当)が形成され、端の方で収束境界(海溝に相当)が形成されている。海溝では、低温のプレートがマントル内部に沈み込んでいる様子が分かる。このプレート境界の形成によって水平方向に大きなスケールを持つプレートの運動が起こり、その沈み込みによって実際の地球マントルのように大規模スケールの温度構造を作り出す。このように、マントル対流のシミュレーションでは、マントルの対流運動のみならず、実際の地球のプレート運動に似た表層運動も再現することが可能である。三次元球殻のモデルでも同様の結果が得られることが分かっている。

図1 粘性率の温度依存性と降伏応力を考慮した三次元矩形型内のマントル対流のシミュレーションの結果[文献1]。左の列は粘性率の分布、右の列はマントルの低温部分の領域を表す。(a)降伏応力が十分に小さい場合、(b)降伏応力が適正な値の場合、(c)降伏応力が十分に大きい場合。
マントル対流でプレート運動を作り出すことは、物理的に言えば、速度場のトロイダル成分(水平方向の回転運動)を作り出すことと同義である(図2)。一方、ポロイダル成分はマントル対流の上下運動を表す。一様な粘性率、あるいは、深さのみに変化する粘性率をもつマントル対流の速度場は、ポロイダル成分のみで、トロイダル成分は存在しないことが数学的に証明されている[文献4]。この場合、円筒状の上昇プルームの周囲をシート状の下降プルームが取り囲むようなパターンになり、表層では上昇プルームの先端から周囲の下降プルームに向かう水平方向の流れが生じるだけなので、実際の地球のような流れの横ずれ運動(プレート運動でいえば、トランスフォーム断層)は再現されない。そこで、粘性率が水平方向に変化する効果を加えることで、速度場のトロイダル成分が生まれる。現在の地球のプレート運動を解析すると、トロイダル成分の強さはポロイダル成分の1/3程度であることが分かっている。
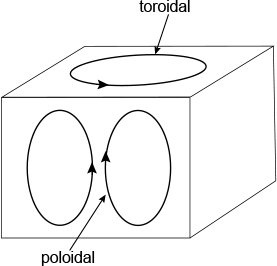
図2 速度場のポロイダル成分とトロイダル成分の簡単な模式図[文献2]。
マントル対流のシミュレーションでは、プレートやプレート境界を自発的に生成するモデルに対して、あらかじめプレートを設定した状態を初期状態として、プレートの沈み込みを再現するモデリングも古くから行われている。このような研究は、多くの場合、マントルの一部を切り出した二次元や三次元のモデルを用いてシミュレーションされる。
図3は、プレートの沈み込みを再現する二次元矩形のマントル対流のシミュレーション[文献5]で、右側のプレートが沈み込みプレート、左側が上盤プレートに対応し、両方のプレートの間の海溝に相当する部分には断層を設置し、そこから沈み込みが起きるように設定されている。上盤プレートと海溝の位置が自由に移動できる場合(図3a)には、海溝が後退し、沈み込むプレートがマントル遷移層下部で横たわっている様子が再現されている。一方、上盤プレートと海溝の位置が固定された場合(図3b)では、プレートはほぼ垂直に沈み込んでいることがわかる。このように、海溝の移動の方向によって、沈み込むプレートの形態が大きく変わり、実際の地球では、前者は例えば、日本海溝、後者はマリアナ海溝に相当する。このシミュレーション結果が示すとおり、後退する日本海溝で沈み込んだプレートはマントル遷移層下部で横たわって、いわゆるスタグナントスラブを形成し、一方、前進するマリアナ海溝で沈み込んだプレートは、マントル遷移層にほぼ垂直に沈み込んでいることが、地震波トモグラフィーによる解析から分かっている。

図3 プレートの沈み込みを再現する二次元矩形のマントル対流のシミュレーション[文献5]。(a)は上盤プレートと海溝の位置が自由に移動できる場合で、(b)は上盤プレートと海溝の位置が固定された場合。カラーコンターは温度を表す。上から下へ時間が経過する。.
以上のように、マントル対流のシミュレーションでは、実際の地球のプレート運動に似た表層運動が自発的に再現される地球物理学的条件を探求するためのモデルや、プレートの沈み込み帯がある場合に、沈み込んだプレートがマントル深部でどのように振る舞うかを調べるためのモデルなど、必要に応じてモデルを使い分けて研究が進められている。