マントル対流の動画

縦横比1：1の矩形内における粘性率が一定のマントル対流。レイリー数（Ra）の違い

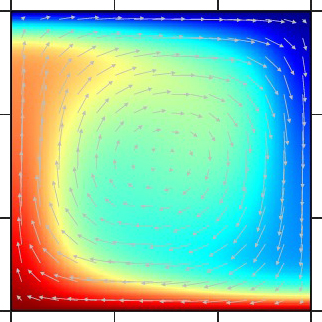
Ra = 104
Ra = 105
Ra = 106
Ra = 107
対流層の下面から加熱され、上面で冷却されるマントル対流。レイリー数（Ra）を大きくするにつれて、対流パターンが時間的に非定常になり、対流の平均速度（RMS Velocity）が大きくなる。実際の地球マントルのレイリー数（Ra～107）に近づけると、対流の平均速度が実際の地球のプレート運動の速度（数cm/yr）に近づく。

縦横比1：1の矩形内における粘性率が温度に依存するマントル対流。粘性率比（γ）の違い

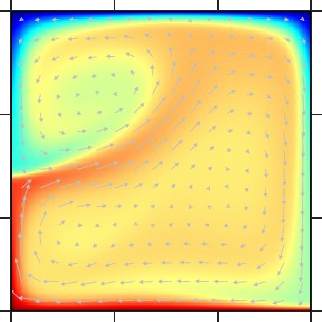
γ = 101
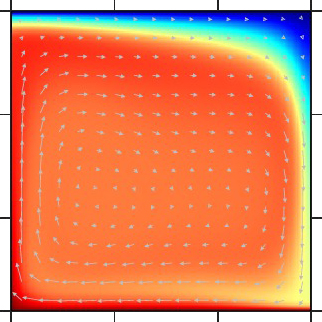
γ = 102
γ = 103
γ = 104
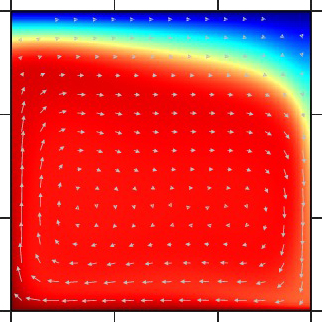対流層の下面から加熱され、上面で冷却されるマントル対流。対流層の上面と下面の粘性率比（γ）を大きくするにつれて、上面に高粘性の厚い熱・力学境界層(リッド）が発達する。このリッドは実際の地球のリソスフェアに相当する。γが103以上では、マントル対流はリッドの下のみで起こるようになる。

縦横比1：4の矩形内における粘性率一定のマントル対流。加熱モードの違い

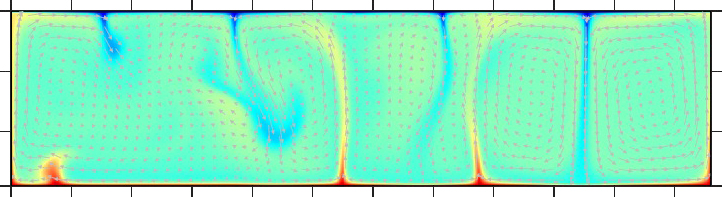
下面加熱のみ
内部加熱のみ
マントルの加熱源が下面加熱のみの場合（左）と内部発熱（発熱量は3.50×10-12 W/kg）のみの場合（右）のマントル対流。レイリー数は107。下面加熱のみではマントルの下降プルームと上昇プルームの両方が存在するが、内部発熱のみでは上昇プルームは存在しない。実際の地球マントルは下面加熱と内部加熱の両方が存在する。
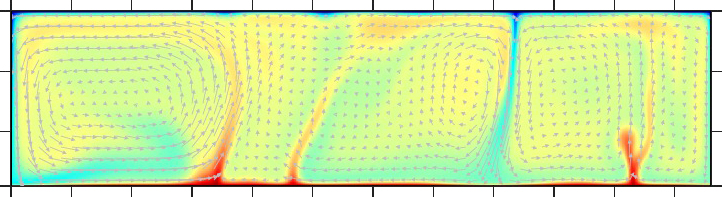
下面加熱と内部発熱（現在）の両方
下面加熱と内部発熱（太古代）の両方
マントルの加熱源として下面加熱と内部発熱の両方が存在する場合のマントル対流。レイリー数は107。左は、マントル内の放射性元素の壊変による内部発熱量が現在の地球マントルの値（3.50×10-12 W/kg）の場合。右は、内部発熱量が30億年前（太古代）の地球マントルの値（1.30×10-11 W/kg）の場合。内部発熱量が大きいほど、マントルの平均温度と上昇プルームの温度の差が小さくなり、下降プルームが卓越するようになる。

二次元極座標モデルでのマントル対流：相変化の効果と粘性率の圧力（深さ）依存性の効果

410km相変化と660km相変化の効果
相変化＋660km相転移面での粘性率ジャンプの効果
相変化＋下部マントル内で粘性率が深さに従い徐々に増加する効果
動画（13.4MB）
動画（13.4MB）
動画（13.4MB）
410km相変化のクラペイロン勾配（γ）と相浮力パラメータ（P）は、γ=+2.0MPa/K、P=2.0、 610km相変化のクラペイロン勾配（γ）と相浮力パラメータ（P）は、γ=-2.5MPa/K、P=1.4 410km相変化と660km相変化のパラメータは左に同じ。下部マントルの粘性率は上部マントルの粘性率の50倍 410km相変化と660km相変化のパラメータは左に同じ。下部マントル最下部の粘性率は下部マントル最上部の粘性率の50倍

三次元球殻内のマントル対流

レイリー数＝7×103、「六面体型」定常対流
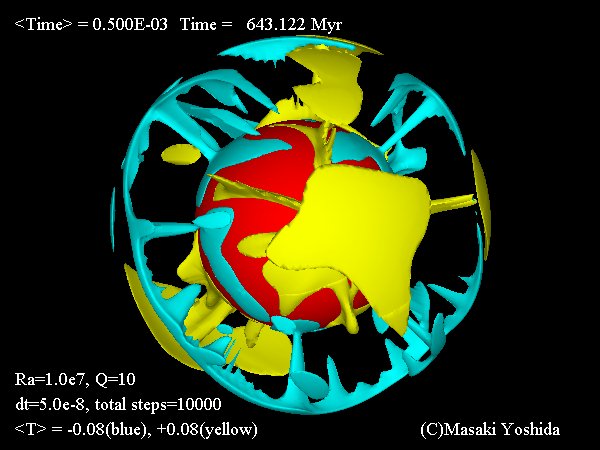
レイリー数＝107、無次元内部発熱量＝10
動画（0.96MB）
動画（5.56MB）
無次元温度0.5の等温度面（緑色）。 黄色と緑色の等値面は各深さでの平均温度との差（温度異常、δT）を表す。 黄色はδT＝＋0.08、水色はδT＝－0.08。中心の赤い球はコアの位置。

マントル対流とコア対流のカップリング（粘性率が桁で異なる二層対流システム）
動画（16MB）
マントル（高粘性層）とコア（低粘性層）の粘性率比が3桁の場合（Yoshida and Hamano, 2016; Yoshida et al., 2017）。

マントルプルームの発生

粘性率が空間的に一定
上部・下部マントルの粘性率比が約60倍
動画（3.9MB）
動画（4.2MB）
透明の黄色の等値面は温度が1250℃、橙色（透明の黄色の内側にある赤色）の等値面は温度が1500℃、青色の等値面は温度異常が－250℃。 透明の黄色の等値面は温度が1375℃、橙色（透明の黄色の内側にある赤色）の等値面は温度が1625℃、青色の等値面は温度異常が－250℃。