吉田 晶樹　ウェブページ

地球物理学

沈み込みカルキュレーター（試用版）

紹介

　マントルの粘性コーナー流モデル（McKenzie, 1969）（図1）を用いて、任意の沈み込みの角度（傾斜角）に対して、「弧側コーナー」（マントルウェッジ）と「海側コーナー」（サブスラブマントル）のそれぞれで沈み込みプレートの表面にかかる流れ圧力、それによる揚力トルクを自動的に計算します。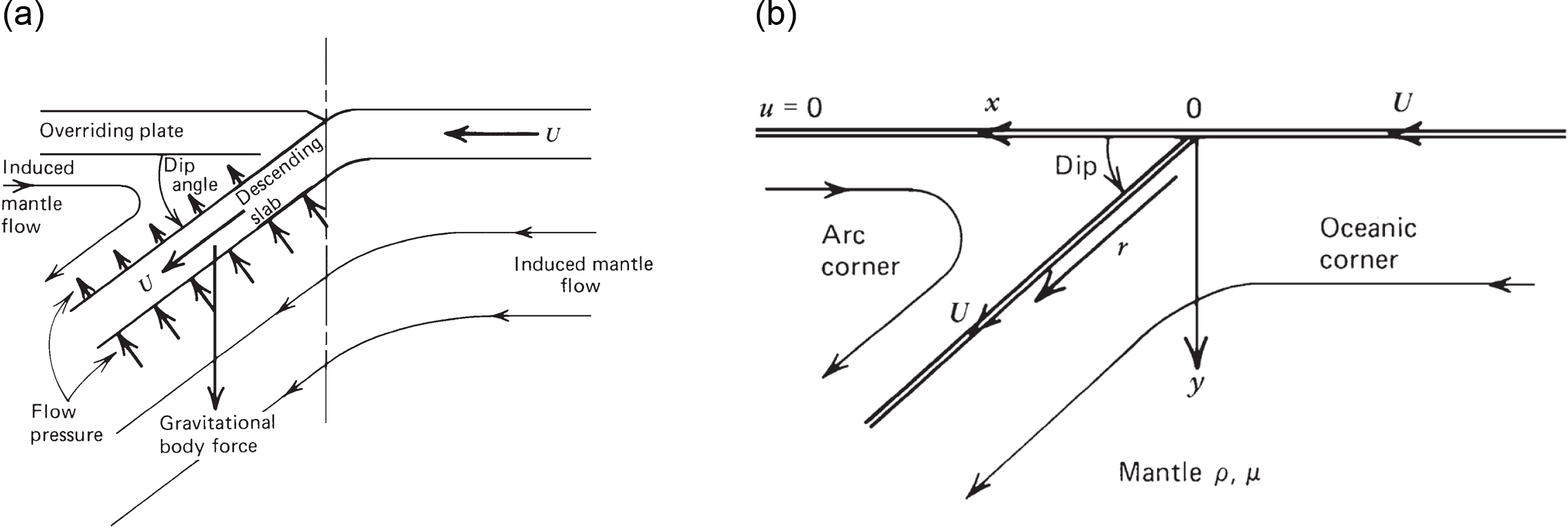



図1．マントルの粘性コーナー流モデル（Turcotte and Schubert, 2014）。左側の上盤プレートの下に右側からもう一方のプレートが速度Uで沈み込んでいる。(a)沈み込み帯でのマントルの流れの概略図。(b)解析のために(a)を模式化した図．Arc cornerを「弧側コーナー」、Oceanic cornerを「海側コーナー」、沈み込みプレートの傾斜角（dip）をθ、「海溝点」をx＝0、y＝0の位置、「沈み込み線」を海溝点から傾斜角θをもって上盤プレート側に伸びる線とする。

解析

　沈み込みプレートの傾斜角（θ）を入力して、沈み込み線上の任意の地点（x_p, y_p）に働く流れ圧力や揚力トルクを求めてみよう。θ以外のパラメータはとりあえずそのままでよい。

手順１：パラメータ入力

• 沈み込み線の傾斜角（θ）：°　（0°＜θ≦90°）
• 沈み込みプレートの速度（U）： cm yr^-1　（例：太平洋、ココス、ナスカプレート）
• 海溝点から沈み込み線に沿った距離（r）： km　（通常、100 km≦r≦500 km）
• マントルの粘性率の常用対数（log₁₀(μ)）：　（例では、μ＝10²¹ Pa s）
• ［変更の必要なし］マントルの密度（ρ）： kg m^-3
• ［変更の必要なし］沈み込みプレートの厚さ（h）： km
• ［変更の必要なし］重力加速度（鉛直下方が正）（g）： m s^-2

手順２：

• 求めたい地点の海溝点からの水平距離（x_p＝rcos(θ)）： km
• 求めたい地点の海溝点からの鉛直距離（y_p＝rsin(θ)）： km
• 求めたい地点の水平速度（u_p＝Ucos(θ)）： cm yr^-1
• 求めたい地点の鉛直速度（v_p＝Usin(θ)）： cm yr^-1

手順３：解析結果

• 弧側コーナーでプレート上面に働く流れ圧力（P_arc）： MPa *¹⁾
• この流れ圧力の無次元値（P'_arc＝P_arc・r/(μU)）：
• 単位面積あたりの揚力トルク（N_arc＝rP_arc）： ×10¹³ N m^-1
• 海側コーナーでプレート下面に働く流れ圧力（P_oce）： MPa *²⁾
• この流れ圧力の無次元値（P'_oce＝P_oce・r/(μU)）：
• 単位面積あたりの揚力トルク（N_oce＝rP_oce）： ×10¹³ N m^-1
• 両コーナーの流れ圧力の合力（P_lif＝P_arc－P_oce）： MPa *¹⁾
• その無次元値（P'_lif＝P'_arc－P'_oce）：
• 単位面積あたりのトルク（N_lif＝N_arc－N_oce）： ×10¹³ N m^-1
• 両コーナーの流れ圧力の比（|P_arc|/P_oce）：
• ［参考］沈み込みプレートにかかる重力トルクとの比較
• 単位面積あたりの重力トルク（N_gra）： ×10¹³ N m^-1 *³⁾
• 重力トルクと揚力トルクの和（N_gra＋N_lif）： ×10¹³ N m^-1 *⁴⁾
• 揚力トルクの絶対値と重力トルクとの比（|N_lif|/N_gra）： *⁵⁾

　　

註釈

*1)　値が負のときプレートを持ち上げる

*2)　値が正のときプレートを持ち上げる

*3)　N_gra＝ρhgsin(θ)・r

*4)　値が正のときプレートは垂れ下がり、正のとき持ち上がる

*5)　値が1より大きいとき揚力トルクが重力トルクよりも大きくプレートは持ち上がる（N_lifがθによらず常に負の場合）

参考文献

| Top | トップページ | 資料 |